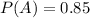We should begin by counting how many letters the word "supercalifragilisticexpialidocious" has.
We'll use a text processor or online resource to avoid making mistakes. While we're at it, we'll also count how many vowels the word has, as that is something we're interested in.
As we can see, the word has 34 characters and 16 vowels.
Now that we know the numbers we're working with, let's analyze how to determine the probability of drawing at least one vowel from the bag.
This would be the same as of subtracting the probability of the complementary event from 1. In this case, the complementary event would be not drawing a vowel in 3 draws, or drawing a consonant on each of the three draws.
We'll call this event B.
This is much easier than the alternative, which would be calculating the probability of drawing exactly one vowel, plus the probability of drawing exactly two vowels, plus the probability of drawing three vowels.
Since we are replacing the letter we draw each time we draw a new one, we can consider the events to be independent.
The probability of drawing a consonant is 18/34=9/17, as there are 18 consonants and 34 total letters.
Since we do this three times, the probability will be
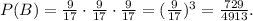
As a reminder, this is the probability of not drawing a single vowel in any of the three draws, so the probability of drawing at least one vowel in three draws (let's call this event A) is:

Using a calculator, we'll get:
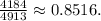
And so, rounding to two decimal places,