Question

1.P lies in the interior of 4ABC. m ABP =3x+7, m4PBC = x+3, and m 4ABC=6x-10What is the measure of PBC?a. 10b. 13c. 37d. 50

Answer 1

Answer: b.13

Step-by-step explanation:

We have that P lies in the interior of the angle ABC, we can represent that as follows:

Where we have the angle ABC and P is in the interior of that angle.

Now, we are told that ABP = 3x+7, and PBC =x+3. We can represent this as follows:

And also, the whole angle ABC has a measure of: ABC = 6x-10

So the sum of the two angles in the image, must be equal to 6x-10:

`\begin{gathered} \text{ABC}=\text{ABP}+\text{PBC} \\ 6x-10=3x+7+x+3 \end{gathered}`

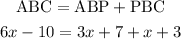
And we solve this equation for x combining like terms:

`6x-10=4x+10`

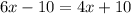
we add 10 to both sides of the equation:

`\begin{gathered} 6x-10+10=4x+10+10 \\ 6x=4x+20 \\ 6x-4x=20 \\ 2x=20 \end{gathered}`

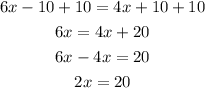
And divide both sides by 2:

`\begin{gathered} x=(20)/(2) \\ x=10 \end{gathered}`

Now that we have the value of x, we can find the value of PBC which is x+3:

`PBC=x+3=10+3=13`

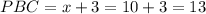
Answer: b.13