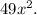Final Answer:
B.
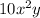
Step-by-step explanation:
The expression
 simplifies as follows:
simplifies as follows:
![\[ (49x^2)|(27y^0) = (7x)^2 * 3^0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/gytnep1ez8ta0qwzchkwf4qb3ketai00fb.png)
Any non-zero number raised to the power of zero is always 1, so
 Thus, the expression further simplifies to:
Thus, the expression further simplifies to:
![\[ (7x)^2 * 1 = 49x^2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/l70z5odwpykcpsqfy1alpj0fdfe6tv0z0r.png)
Now, the expression is reduced to
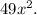 To find an equivalent expression, we observe that
To find an equivalent expression, we observe that
 is the same as
is the same as
 which can be factored as
which can be factored as
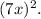
Therefore, the equivalent expression is \(10 \times
 , and this can be further simplified to
, and this can be further simplified to
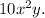
In conclusion, the final equivalent expression is
 , which corresponds to option B. The key steps in the simplification involve recognizing the power of zero rule and factoring
, which corresponds to option B. The key steps in the simplification involve recognizing the power of zero rule and factoring