Question

For #4 and #5, write the equation of the quadratic using the best form, vertex: y = a(x – h)2 + k or intercept y = a(x - p)(x -9),

Answer 1

1)

Given,

The coordinates of the vertex, (h, k)=(2, -4).

The coordinates of a point through which the graph passes, (x, y)=(0,0).

The vertex form of the quadratic equation for the graph is,

`y=a(x-h)^2+k\ldots\ldots.(1)`

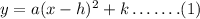
Here, (h, k) is the coordinates of the vertex of the graph.

Put the values of h, k, x and y in the above equation to find the value of a.

`\begin{gathered} 0=a(0-2)^2-4 \\ 0=a*4-4 \\ 4=4a \\ (4)/(4)=a \\ 1=a \end{gathered}`

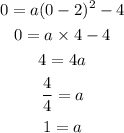
Now, put the values of h, k and a in equation (1) to obtain the vertex form of the quadratic equation whose graph has vertex (2, -4) and passing through point (0, 0).

`\begin{gathered} y=1*(x-2)^2-4 \\ y=(x-2)^2-4 \end{gathered}`

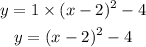
So, the vertex form of the quadratic equation whose graph has vertex (2, -4) and passing through point (0, 0) is,

`y=(x-2)^2-4`

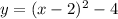
2)

From the graph, the coordinates of a point through which the graph passes is (x,y)=(-2, -4).

The intercept form of a quadratic equation is,

`y=a(x-p)(x-q)\text{ ------(1)}`

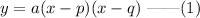
Here, p and q are the x intercepts.

From the graph, the x intercepts are p=-3 and q=2.

Now, put the values of x, y, p and q in the above equation to find the value of a.

`\begin{gathered} -4=a(-2-(-3))(-2-2) \\ -4=a(-2+3)(-4) \\ -4=a*1*(-4) \\ a=1 \end{gathered}`

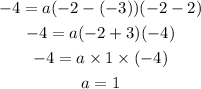
Now, put the a values of. a, p and q in equation (2) to find the intercept form of quadratic function of the graph.

`\begin{gathered} y=1*(x-(-3))(x-2) \\ y=(x+3)(x-2) \end{gathered}`

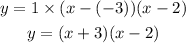
Therefore, the intercept form of quadratic function of the graph is y=(x+3)(x-2).