Question

Consider the following function.

r(x)
|x|
Step 2 of 2: Find two points on the graph of this function, other than the origin, that fit within the given [-10, 10] by [-10, 10] grid.
Express each coordinate as an integer or simplified fraction.

Answer 1

The coordinates of two points on the graph of this function that fit within the given [-10, 10] by [-10, 10] grid are:

A = (-8, -3)

B = (8, -3)

In Mathematics and Euclidean Geometry, the vertex form of the equation for an absolute value function can be modeled by the following:

y = a|x - h| +k.

Where:

• h and k are the vertex of the graph.
• a is a numerical constant.

Based on the given absolute value function
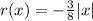`r(x)=-(3)/(8) |x|`, we would evaluate it when x equals -8 and 8 as follows;

`r(x)=-(3)/(8) |x|\\\\r(-8)=-(3)/(8) * |-8|\\\\r(-8)=-(3)/(8) * 8`

r(-8) = -3

When x is 8, the output value of r(x) can be calculated as follows;

`r(x)=-(3)/(8) |x|\\\\r(8)=-(3)/(8) * |8|\\\\r(8)=-(3)/(8) * 8`

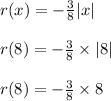
r(8) = -3

Complete Question;

Consider the following function.

`r(x)=-(3)/(8) |x|`

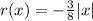
Step 2 of 2: Find two points on the graph of this function, other than the origin, that fit within the given [-10, 10] by [-10, 10] grid.

Express each coordinate as an integer or simplified fraction.