Question

The total amount spent by some number of people on clothing and footwear In the years 2000-2009 can be modeled by the quadratic function. Where x=0 represents January 1, 2000, x=1 represents January 1, 2001, and so on, and f(x) is in billions of dollars. According to the model, in what year during this period was the amount of clothing and footwear a maximum In the year (blank) , (blank) billion was spent on clothing and footwear.

Answer 1

The maximum spending occurred in the year 2008.

To find the year during which the amount of clothing and footwear spending was at a maximum according to the given quadratic model
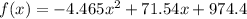`\( f(x) = -4.465x^2 + 71.54x + 974.4 \)`, where x = 0 represents January 1, 2000, x = 1 represents January 1, 2001, and so on, and f(x) is in billions of dollars, we follow these steps:

1. The vertex of the parabola represented by the quadratic equation
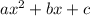`\( ax^2 + bx + c \)` occurs at
`\( x = -(b)/(2a) \).`

2. We calculate the vertex using the coefficients a = -4.465 and b = 71.54 from the quadratic equation.

3. The year of the maximum spending is found by adding 2000 to the x-coordinate of the vertex since x = 0 corresponds to the year 2000.

4. The maximum spending is simply the value of the function f(x) at this x-coordinate.

According to the calculation, the maximum spending occurred in the year 2008, and the amount spent on clothing and footwear in that year was approximately 1261 billion dollars.

Answer 2

For this problem, we are given a quadratic equation that models the total amount spent on clothing and footwear in the years 2000-2009. We need to use the model to determine the maximum amount spent during the period.

The equation is shown below:

`f(x)=-4.462x^2+71.54x+97.44`

Since the leading term is negative, the vertex of this function will represent an absolute maximum value. Therefore we can determine the vertex to answer the problem, the vertex's coordinates are given below:

`\begin{gathered} x_(max)=(-b)/(2a)\\ \\ y_(max)=f(x_(max)) \end{gathered}`

Then we have:

`\begin{gathered} x_(max)=(-71.54)/(2\cdot(-4.462))=8.017\\ \\ y_(max)=-4.462\cdot(8.017)^2+71.54\cdot(8.017)+97.44=384.2 \end{gathered}`

In the year 2008, 384 billion was spent on clothing and footwear.