Question

Consider C(-6,-1) and D(4,8). Point P3 partitions the segment from C to D in a 1:2 ratio. Find the coordinates of point P3.

a) P3(2, 3.5)
b) P3(-2, 3.5)
c) P3(-2, -3.5)
d) P3(2, -3.5)

Answer 1

To find the coordinates of point P3, which partitions the segment CD in a 1:2 ratio, we can use the section formula. The coordinates of P3 are (
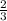`(2)/(3)`, 5). None of the given options exactly matches this result.

Step-by-step explanation:

To find the coordinates of point P3, which partitions the segment CD in a 1:2 ratio, we can use the section formula. The section formula states that for two points A(x₁, y₁) and B(x₂, y₂) dividing a line segment in the ratio m:n, the coordinates of the dividing point P(x, y) are given by:

x =
`(mx_2 + nx_1)/(m + n)`

y =
`(my_2 + ny_1)/(m + n)`

In this case, we want P3 to divide the segment CD in a 1:2 ratio. So, m = 1 and n = 2.

x =
`(2 \cdot 4 + 1 \cdot (-6))/(1 + 2)`

=
`(8 - 6)/(3)`

=
`(2)/(3)`

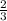
y =
`(2 \cdot 8 + 1 \cdot (-1))/(1 + 2)`

=
`(16 - 1)/(3)`

=
`(15)/(3)`

= 5

Therefore, the coordinates of P3 are (
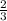`(2)/(3)`, 5). None of the given options exactly matches this result.