Question

Write an equation for the line that passes through (-4,1) and (-8,6)

Answer 1

`y=- (5)/(4)x-4`

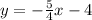
Explanation:

1) if the A has coordinates (-4;1) and B - (-8;6), then it is possible to write the formula of the required line:

`(X-X_A)/(X_A-X_B) =(Y-Y_A)/(Y_B-Y_A);`

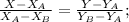
2) if to substitute the coordinates given in the condition, then:

`(X+4)/(-8+4) =(Y-1)/(6-1);`

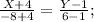
3) finally, the required equation of the line is:

-4y=5x+16; ⇔y= -5/4 x-4 (slope-intersection form)

PS. note, the suggested solution is not the only one.