We are given that a person can bicycle 26 miles in the same time it takes to walk 6 miles. If we say that "x" is the walking speed in mph then since he can ride 10 mph faster than we can walk we have the following relationship:
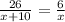
this relationship comes from the fact that the velocity is defined as the distance over time, like this:
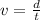
Since we are given that times are equal, then if we solve for the time we get:
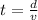
Therefore, the distance over the velocity gives us the time and since the times are equal, we get the relationship. Now we can solve for "x" by cross multiplying:

Now we apply the distributive property on the right side:
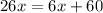
Now we subtract 6x from both sides:
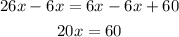
Now we divide both sides by 20:
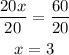
Therefore, the walking speed is 3 mph. Now we need to determine the time it takes to walk 35 miles. We do that applying the formula for the time we got previously:
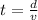
Plugging in the values we get:
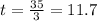
therefore, the time is 11.7 hours.