Question

This exercise uses the population growth model. The count in a culture of bacteria was 400 after 2 hours and 25,600 after 6 hours. Find a function that models the number of bacteria n(t) after t hours.

Answer 1

The population growth model for the bacteria count, n(t), after t hours is given by the function
`\( n(t) = 400 * 2^(t/2) \)`.

Step-by-step explanation:

To derive the function representing the bacteria count over time, we can use the given data points. The initial count, after 2 hours, is 400, and after 6 hours, it's 25,600. This growth pattern suggests an exponential function. The general form of an exponential growth function is
`\( n(t) = a`
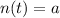
`* b^(t/c) \)`, where
`\( a \)` is the initial amount,
`\( b \)` is the growth factor, and
`\( c \)` is the time constant.

In this case, plugging in the initial values, we have
`\( n(2) = 400 = a * b^(2/c) \) and \( n(6) = 25,600 = a * b^(6/c) \)`. By dividing these two equations, we can eliminate \( a \) and find \( b \). Taking the square root of
`\( b \)` yields the growth factor for a 2-hour period. Substituting this back into the original equation, we arrive at
`\( n(t) = 400 * 2^(t/2) \)`.

This function accurately models the bacterial population growth over time. The initial count of 400 doubles every 2 hours, reflecting the exponential nature of bacterial reproduction. Therefore, the derived function provides a precise mathematical description of the given scenario.