Given the table:
Number of pairs of shoes 4 5 6 7 8 9 10
Frequency 6 11 11 9 8 9 7
Let's solve for the following:
• (a). The mean
To find the mean, we have:
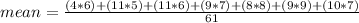
Solving further:
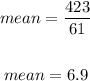
The mean is 6.9
• (b). The median
The median is the middle value.
To find the median, we have:

The median will be the 31st number.
From the table, the 31st number is = 7
Therefore, the median is 7
• (C). The sample standard deviation
To find the standard deviation, apply the formula:
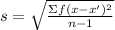
Thus, we have:
![\begin{gathered} s=\sqrt{(6(4-6.9)^2+11(5-6.9)^2+11(6-6.9)^2+9(7-6.9)^2+8(8-6.9)^2+9(9-6.9)^2+7(10-6.9)^2)/(61-1)} \\ \\ s=√(3.59683) \\ \\ s=1.9 \end{gathered}]()
The standard deviation is 1.9
• (d). The first quartile.
The first quartile is the median of the lower half of the data.
To lower half of data is from 1 to 30th data.
The median of the lower half will be:
![(30)/(2)=15]()
This means the value in the 15th frequency is the lower quartile.
The value in the 15th frequency is 5.
Therefore, the first quartile is 5.
• (e). Upper quartile
This is the median of the upper half of the data.
The median is the frequency from 32 to 61 frequency.
The median will be:
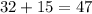
The 47th data.
The value of the 47th data is 9
Therefore, the third quartile is 9.
• (f). What percent have at least 5 pairs of shoes?
Only 6 respondents have less than 5 pairs of shoes.
To find the percent with at least 5 pairs of shoes, we have:
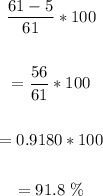
• (g). 28% have fewer than how many pairs of shoes?
28% have fewer than 6 pairs of shoes.
ANSWER:
• Mean = 6.9
,
• Median = 7
,
• Standard deviation = 1.9
,
• First quartile = 5
,
• Third quartile = 9
,
• At least 5 pairs = 91.8%
,
• 28% have fewer than, ,6 pairs of shoes.