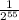Question

$$\frac{1}{2^{1}} \frac{1}{2^{2}} \frac{1}{2^{3}} \cdots \frac{1}{2^{8}} \frac{1}{2^{9}} \frac{1}{2^{10}}?$$

Answer 1

The given expression
`(1)/(2^(1) ) *(1)/(2^(2) ) *(1)/(2^(3) ) ...*(1)/(2^(8) ) *(1)/(2^(9) ) *(1)/(2^(10) )` is simplified to give
`(1)/(2^(55) )`

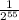
To simplify the given expression:

`(1)/(2^(1) ) *(1)/(2^(2) ) *(1)/(2^(3) ) ...*(1)/(2^(8) ) *(1)/(2^(9) ) *(1)/(2^(10) )`

you can combine the terms by adding the exponents:

=
`(1)/(2^(1+2+3+..+8+9+10) )`

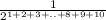
By using the formula for the sum of the first n positive integers, which is;

n(n + 1)/2

where n = 10

= 10(10 + 1)/2

= 10(11)/2

= 110/2

= 55

So, given expression
`(1)/(2^(1) ) *(1)/(2^(2) ) *(1)/(2^(3) ) ...*(1)/(2^(8) ) *(1)/(2^(9) ) *(1)/(2^(10) )` is simplified to
`(1)/(2^(55) )`