Question

A rectangular field is to be fenced on three sides with 1000 meters of fencing. The fourth side is a straight river's edge that will not be fenced. Use Desmos to help get your answerFind the dimensions of the field that will maximize the area of the enclosure. _____ meters X ____ metersWhat is this maximum area of the enclosure? _____ squared meters

Answer 1

First, let's find a function that will give us the area with for the dimensions.

Since the area is rectangular, let two sides be x and the other be y:

This means that the sum of these three sides have to be equal to 1000 meters:

`\begin{gathered} x+y+x=1000 \\ y+2x=1000 \\ y=1000-2x \end{gathered}`

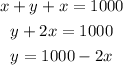
Also, the area of the rectangle is:

`\begin{gathered} A(x,y)=xy \\ A(x)=x(1000-2x) \\ A(x)=1000x-2x^2 \\ A(x)=-2x^2+1000x \end{gathered}`

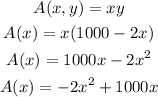
This is a quadratic function and, since its leading coefficient is negative, it has a maximum value at its vertex. The x value of the vertex corresponds to the x variable of the function, and the y value corresponds to the maximum value of the function A(x).

The x coordinate of the vertex of a quadratic function is:

`\begin{gathered} x_V=-(b)/(2a) \\ x_V=-(1000)/(2(-2)) \\ x_V=-(1000)/(-4) \\ x_V=250 \end{gathered}`

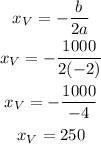
So, the value of x for which the field has maximum area is 250, which means that the other side of the field is:

`\begin{gathered} y=1000-2x \\ y=1000-2\cdot250 \\ y=1000-500 \\ y=500 \end{gathered}`

So, the field will have maximum area when its dimensions are 250 meter x 500 meters.

The y value of the vertex can be calculated inputting the x value into the funciton, so:

`\begin{gathered} A_(\max )=A(x_V)=-2(250)^2+1000\cdot250 \\ A_(\max )=-2\cdot62500+250000 \\ A_(\max )=-125000+250000 \\ A_(\max )=125000 \end{gathered}`

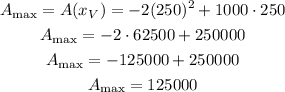
So, the maximum are of the field will be 125000 squared meters.