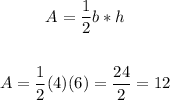Question

What is the area of a triangle hint make use of the midpoint formula if a triangle is isosceles

Answer 1

To find the area of the given triangle:

1. Find the length of each side, use the next formula to find the distance between two points:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

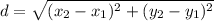
Distance between points (6,3) and (4,9):

`\begin{gathered} d=√((4-6)^2+(9-3)^2) \\ d=\sqrt{(-2)\placeholder{⬚}^2+6^2} \\ d=√(4+36) \\ d=√(40) \end{gathered}`

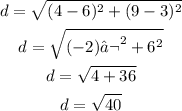
Distance between points (4,9) and (8,9):

`\begin{gathered} d=\sqrt{(8-4)\placeholder{⬚}^2+(9-9)\placeholder{⬚}^2} \\ d=√(4^2+0) \\ d=√(4^2) \\ d=4 \end{gathered}`

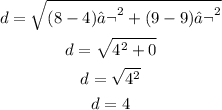
Distance between points (8,9) and (6,3):

`\begin{gathered} d=\sqrt{(6-8)\placeholder{⬚}^2+(3-9)\placeholder{⬚}^2} \\ d=\sqrt{(-2)\placeholder{⬚}^2+(-6)\placeholder{⬚}^2} \\ d=√(4+36) \\ d=√(40) \end{gathered}`

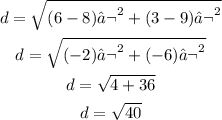
It is a isosceles traingle (have two sides of equal length), use the midpoint formula to find the middle of the base (the base is the side with different length):

`\begin{gathered} M((x_1+x_2)/(2),(y_2+y_1)/(2)) \\ \\ (4,9)(8,9) \\ M((4+8)/(2),(9+9)/(2))=M((12)/(2),(18)/(2))=M(6,9) \end{gathered}`

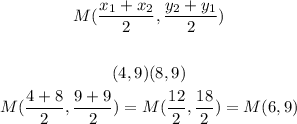
Find the height of the triangle by finding the distance between Midpoint of the base and the other point (The points that is not part of the base) (6,3):

`\begin{gathered} d=\sqrt{(6-6)\placeholder{⬚}^2+(9-3)\placeholder{⬚}^2} \\ d=√(0+6^2) \\ d=√(6^2) \\ d=6 \end{gathered}`

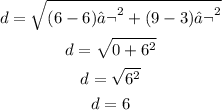
Then, the area of the triangle is: 12 square units

`\begin{gathered} A=(1)/(2)b*h \\ \\ A=(1)/(2)(4)(6)=(24)/(2)=12 \end{gathered}`