We are given that the position of an object is given by the following function:
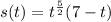
We are asked to determine the interval where the object is speeding up or slowing down.
The object will speed up if the velocity and the acceleration have the same sign and it will slow down if the velocity and acceleration have opposite signs.
Therefore, we need to determine the function of the velocity of the object. To do that we will first, determine the derivative of the position function with respect to time:
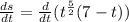
Now, we apply the distributive law:
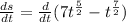
Now, we distribute the derivative operator:

Now, we apply the following rule of derivatives:
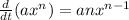
Applying the rule we get:
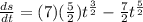
Simplifying:
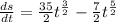
Thus we get the function for the velocity. Now, we set the velocity to zero to determine the points where the velocity changes directions:
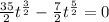
We take (7/2)(t^3/2) as a common factor:
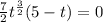
Now, we set each factor to zero:

For the second factor:
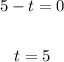
Therefore, the velocity changes direction at "t = 5". We pick a number between 0 and 5 to determine the sign of the velocity in that interval. We choose "t = 1" and substitute in the function for velocity:
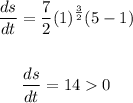
Therefore, the velocity is positive for values between 0 and 5 and negative between 5 and 20.
Now, we determine the acceleration by derivating the velocity function:
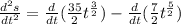
Applying the rule we get:
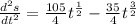
Now, we take (35/4)t^1/2 as a common factor:
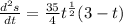
Now, we set the acceleration to zero:
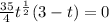
We set each factor to zero:
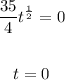
For the second factor we get:

Now, we pick a value between 0 and 3. we can choose t = 1 and substitute in the function for acceleration:

Therefore, the acceleration is positive between 0 and 3 and negative between 3 and 20. Now, we determine where the two functions have the same sign and where they have opposite signs. We can draw the following diagram:
Therefore, the object is speeding up in the interval between 0 and 3 and between 5 and 20. We write this as follows:
[tex]\begin{gathered} Speeding\text{ up} \\ 0The object is slowing down in the interval between 3 and 5. We write this as follows:[tex]\begin{gathered} slowing\text{ down} \\ 3