The likelihood of an event is expressed as a number between zero (the event will never occur) and one (the event is certain). For example, the probability of an outcome of heads on the toss of a fair coin is ½ or 0.5.
A single toss of a coin is an event (also called a trial) that is not connected to or influenced by other events. When a coin is tossed twice, the coin has no memory of whether it came up heads or tails the first time, so the second toss of the coin is independent.
In this case we don't have two consecutive tosses, we instead flip two coins. Nevertheless the same rule stated above apply for this case.
Now the proability of something to happen is always 1, this means that the sum of all the possible outcomes have to be equal to 1.
We also need to remember the Product Rule. This states that the probability of the occurrence of two independent events is the product of their individual probabilities. The probability of getting two heads on two coin tosses is 0.5 x 0.5 or 0.25.
With this in mind it is easier to think of this problem like this: The probability of getting one or more heads is equal to 1 minus the probability of obtaining two tails. But this last proability is equal to 0.5 x 0.5=0.25; therefore the probability we are looking for is:
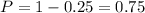
Hence the probability of obtaining one head or more is 0.75.