Question

anthony owns a food truck that sells tacos and burritos. he only has enough supplies to make 130 tacos or burritos. he sells each taco for $4 and each burrito for $8. anthony must sell a minimum of $780 worth of tacos and burritos each day. also l, he can sell a maximum of 20 tacos. if x represents the number of tacos sold and y represents the number of burritos sold, write and solve a system of inequalities qraphically and determine one possible solution.

Answer 1

x represents the number of tacos and each taco costs $4 so the total earnings for selling tacos is 4x

y represents the number of burritos and each one costs $8, so the total earnings for selling burritos is represented as 8y

If you add the earnings of tacos and burritos you get the total earnings of the day 4x+8y

He must sell a minimum of $780, this means that he must earn $780 or more

Symbolically:

`4x+8y\ge780`
`\begin{gathered} 8y\ge780-4x \\ y\ge(780)/(8)-(4x)/(8) \\ y\ge97.5-(1)/(2)x \end{gathered}`

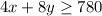
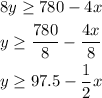
The maximum number of tacos he can sell is 20, this is, 20 tacos or less, you can express this as

`x\leq20`

He only has supplies to make a maximum of 130 tacos or burritos, so that

`\begin{gathered} x+y\leq130 \\ y\leq130-x \end{gathered}`

Plot the three inequalities

One possible solution is where the three shaded areas met, for example he can make 20 tacos and 100 burritos