Question

Help please im so confused

Answer 1

The statements and reasons used to prove
`\overline{BE}` bisects ∠DBC are presented as follows;

Statement Reasons

1.
`\overline{BE}` ║
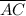`\overline{AC}` Given

`\overline{AC}` ≅
`\overline{BC}`

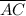2. ΔABC is isosceles Definition

3. ∠A ≅ ∠C Base angles of isosceles triangle
4. ∠DBE ≅ ∠A Corresponding angles theorem

5. ∠EBC ≅ ∠C Alternate interior angles

6. ∠DBE ≅ ∠EBC Transitive property of congruence

7. m∠DBE = m∠EBC Definition of congruent angles

8.
`\overline{BE}` bisects ∠DBC Definition of bisected angle

The details of the reasons used to prove that the segment
`\overline{DE}` bisects angle ∠DBC are as follows;

Definition of isosceles triangles; Isosceles triangles are triangles that consists of a pair of congruent sides and angles

The base angles of an isosceles triangle; The base angles of an isosceles triangle are congruent

Alternate interior angles; Alternate interior angles are angles formed in the interior part of parallel lines and on alternate side of their transversal

Transitive property of congruence; The transitive property of congruence states that if A ≅ B and A ≅ C, then B ≅ C

Definition of congruent angles; Congruent angles are angles that have the same measure

Definition of bisected angles; A bisected angle is an angle that is shared into two congruent angles