Question

Not sure how to do this. Simplify the expression by converting to rational exponents. Assure that all variables represent positive real numbers

Answer 1

We are given the following expression:

`\frac{\sqrt[4]{y^3}}{\sqrt[5]{y^3}}`

To convert to rational exponents we will use the following relationship:

`\sqrt[y]{a^x}=a^{(x)/(y)}`

Applying the relationship we get;

`\frac{\sqrt[4]{y^3}}{\sqrt[5]{y^3}}=\frac{y^{(3)/(4)}}{y^{(3)/(5)}}`

Now, we will use the following property of exponents on the denominator:

`(1)/(a^x)=a^(-x)`

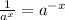
Therefore, we can bring the denominator up by inverting the sign of the exponents, like this:

`\frac{y^{(3)/(4)}}{y^{(3)/(5)}}=y^{(3)/(4)}y^{-(3)/(5)}`

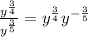
Now, we use the following property of exponents:

`a^xa^y=a^(x+y)`

Applying the property we get:

`y^{(3)/(4)}y^{-(3)/(5)}=y^{(3)/(4)-(3)/(5)}`

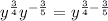
Adding the exponents we get:

`y^{(3)/(4)-(3)/(5)}=y^{(3)/(20)}`

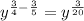
Since we can't simplify any further this is the final answer.