Question

Find the missing coordinate of P , using the fact that P lies on the unit circle in the given quadrant. coordinates QUADRANT P(2/3, ______) II

Answer 1

To find the missing coordinate of point P in quadrant II on the unit circle, use the given x-coordinate and determine the appropriate sign for the missing y-coordinate.

Step-by-step explanation:

To find the missing coordinate of point P, we need to use the fact that P lies on the unit circle in the given quadrant. In quadrant II, the x-coordinate is negative and the y-coordinate is positive. Since the x-coordinate is given as 2/3, the y-coordinate should be positive. Therefore, the missing coordinate of P is (2/3, y), where y is positive.

Answer 2

The missing y-coordinate of point P in the second quadrant, lying on the unit circle with x-coordinate
`\( (2)/(3) \), is \( (√(5))/(3) \)`. Therefore, the coordinates of P are
`\( \left((2)/(3), (√(5))/(3)\right) \).`

Step-by-step explanation:

In the second quadrant of the Cartesian coordinate system, the x-coordinate is negative, and the y-coordinate is positive. Since P lies on the unit circle, the distance from the origin to P is 1.

Given that the x-coordinate of P is
`\( (2)/(3) \)`, we can use the Pythagorean theorem to find the y-coordinate. The Pythagorean theorem states that for any right-angled triangle, the square of the length of the hypotenuse
`(\(c\))` is equal to the sum of the squares of the lengths of the other two sides
`(\(a\) and \(b\)).`

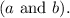
In this case, let (a) be the x-coordinate
`(\( (2)/(3) \))`, (b) be the y-coordinate, and (c) be the distance from the origin to P (which is 1 on the unit circle).

The Pythagorean theorem equation is:

`\[ a^2 + b^2 = c^2 \]`

Substitute the given values:

`\[ \left((2)/(3)\right)^2 + b^2 = 1^2 \]`

`\[ (4)/(9) + b^2 = 1 \]`

Now, solve for \(b\):

`\[ b^2 = 1 - (4)/(9) \]`

`\[ b^2 = (5)/(9) \]`

`\[ b = \pm \sqrt{(5)/(9)} \]`

Since P is in the second quadrant where the y-coordinate is positive, the y-coordinate of P is
`\( (√(5))/(3) \)`.

Therefore, the coordinates of P in the second quadrant are
`\( \left((2)/(3), (√(5))/(3)\right) \).`