Question

A rectangular tank, 25 cm long and 25 cm wide is filled with water to a depth of 10 cm. When a metal cube of edge 10 cm is placed on the tank, the water level rises. Find the height of the new water level.

Answer 1

The problem involves the volume of the water of the rectangular tank, so first we must find the volume of our water. For the volume we have;

`\begin{gathered} \text{Volume = Lenght x Width x Height} \\ V_(water)_{}_{}\text{ = 25 x 25 x 10} \\ V_(water)=6250cm^3 \end{gathered}`

Therefore our tank has an initial volume of 6250 cm³, but if you drop a cube with a side measuring 10 cm. the volume of the water in our tank increases. Giving us the expression;

`\begin{gathered} \text{Volume Combined = Volume of Water + Volume of Cube} \\ V_(comb)=V_(water)+V_(cube) \end{gathered}`

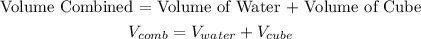
Since we already have the volume of the water (which is 6250), we just need to find the volume of the cube using the same formula (Volume = Lenght x Width x Height);

`\begin{gathered} V_(comb)=V_(water)+V_(cube) \\ V_(comb)=V_(water)+(Lenght_(cube))(Width_(cube))(Height_(cube))_{}_{}_{} \\ V_(comb)=V_(water)+10(10)(10) \\ V_(comb)=6250+1000 \\ V_(comb)=7250cm^3 \end{gathered}`

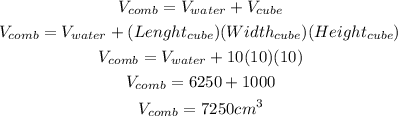
Therefore our new volume when they are combined or when the cube is droped in the tank is 7250 cm³.

But we must remember since our tank would remain it's shape no matter how much water it holds it would always retain it's dimension of it's lenght and width (25x25), therefore it is possible to find the height of the new water level using this logic;

`\begin{gathered} V_(comb)=(Length_(\tan k))(Width_(\tan k))(Height_(water)\text{)} \\ V_(comb)=(25)(25)(Height_(water))\text{ , with our }V_(comb)=7250 \\ 7250=625(Height_(water)) \\ \text{Height}_(water)=(7250)/(625) \\ \text{Height}_(water)=11.6\text{ cm} \end{gathered}`

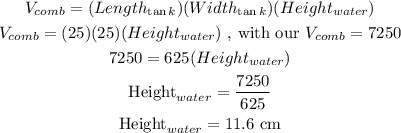
Therefore the height of the new water level is 11.6 cm.