Question

Find the first four terms and the 100 th term of the sequence. aₙ = nᵏ

Answer 1

The first four terms of the sequence
`\(aₙ = nᵏ\) are \(a₁ = 1^k, a₂ = 2^k, a₃ = 3^k, a₄ = 4^k\)`, and the 100th term is
`\(a₁₀₀ = 100^k\).`

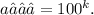
Step-by-step explanation:

In this sequence,
`\(aₙ = nᵏ\), where \(n\)`represents the position in the sequence and (k) is a constant exponent. To find the first four terms, we substitute
`\(n = 1, 2, 3, \text{ and } 4\)` into the formula:

`- \(a₁ = 1^k\)`

`- \(a₂ = 2^k\)`

`- \(a₃ = 3^k\)`

`- \(a₄ = 4^k\)`

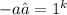
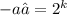
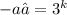
For the 100th term,
`\(a₁₀₀ = 100^k\)`. This means we substitute (n = 100) into the formula.

The sequence demonstrates the growth of (n) raised to the power of (k). The first four terms showcase this progression, starting with
`\(1^k\)` and increasing with each subsequent term. The 100th term,
`\(100^k\)`, reflects the pattern's continuation at the 100th position. The value of (k) determines the nature of the growth – whether it's linear, quadratic, or another form. Understanding these terms provides insights into the behavior of the sequence and its long-term trend, such as its rapid or gradual increase.

In summary, the sequence
`\(aₙ = nᵏ\)` yields its first four terms by substituting
`\(n = 1, 2, 3, \text{ and } 4\)` and the 100th term by substituting (n = 100). This exploration offers a glimpse into the sequence's behavior, determined by the constant exponent (k).