Ryan’s distance from the first floor when he stepped onto the escalator is 1250 centimeters.
In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):
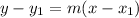
Where:
- x and y represent the data points.
- m represent the slope.
First of all, we would determine the slope of the table;
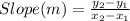
Slope (m) = (980 - 1070)/(9 - 6)
Slope (m) = -90/3
Slope (m) = -30
At data point (15, 800) and a slope of -30, a function for this line can be calculated by using the point-slope form as follows:
y - 800 = -30(x - 15)
y = -30x + 450 + 800
y = -30x + 1250
Therefore, the y-intercept of 1250 cm represents Ryan’s distance from the first floor when he stepped onto the escalator.