Question

Ryan stepped into an escalator moving at a constant rate. The table below shows his distance from the first floor after different amounts of time. What was Ryan’s distance from the first floor when he stepped onto the escalator?_ centimeters

Answer 1

Ryan’s distance from the first floor when he stepped onto the escalator is 1250 centimeters.

In Mathematics and Geometry, the point-slope form of a straight line can be calculated by using the following mathematical equation (formula):

`y - y_1 = m(x - x_1)`

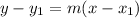
Where:

• x and y represent the data points.
• m represent the slope.

First of all, we would determine the slope of the table;

`Slope(m)=(y_2-y_1)/(x_2-x_1)`

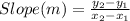
Slope (m) = (980 - 1070)/(9 - 6)

Slope (m) = -90/3

Slope (m) = -30

At data point (15, 800) and a slope of -30, a function for this line can be calculated by using the point-slope form as follows:

y - 800 = -30(x - 15)

y = -30x + 450 + 800

y = -30x + 1250

Therefore, the y-intercept of 1250 cm represents Ryan’s distance from the first floor when he stepped onto the escalator.

Answer 2

step 1

Find the slope or unit rate of the linear equation

take the points

(6,1070) and (9,980)

m=(980-1070)/(9-6)

m=-90/3

m=-3 cm/sec

step 2

Find the equation in pont slope form

y-y1=m(x-x1)

we have

m=-3

(x1,y1)=(6,1070)

substitute

y-1070=-3(x-6)

Convert to slope intercept form

isolate the variable y

y-1070=-3x+18

y=-3x+1088

therefore

the y-intercept or initial value is 1088 cm

the answer is

1088 cm