The maximum height gained by the cube is approximately
 above its initial position.
above its initial position.
How did we get the value?
Let's do the calculations:
Given values:
- L = 20.0 cm
- W = 15.0 cm
- D = 3.0 cm
- k = 800 N/m
- m = 0.150 kg
- s = 6.00 cm
- P = 24.6 kPa
-
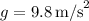
1. Calculate x :
A = L x W
![\[ x = \sqrt{(P \cdot A)/(k)} \]](https://img.qammunity.org/2024/formulas/physics/college/1r8xnl8a5huky6z4pg1npbkdn6qtff8rwj.png)
![\[ A = (0.20 \, \text{m}) * (0.15 \, \text{m}) \]](https://img.qammunity.org/2024/formulas/physics/college/a85ikhsjn6nna4j0nsk83aj0ndvnga24qf.png)
![\[ A = 0.03 \, \text{m}^2 \]](https://img.qammunity.org/2024/formulas/physics/college/qo4cpghrhdhn7bh8d4dgxj18rftq1tpa2c.png)
![\[ x = \sqrt{\frac{(24.6 * 10^3 \, \text{Pa}) * (0.03 \, \text{m}^2)}{800 \, \text{N/m}}} \]](https://img.qammunity.org/2024/formulas/physics/college/lrqsl0vzcjupj09i5xa5nktbmp04ra9o3d.png)
Calculating x:
![\[ x \approx 0.108 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/college/eozueicqvoc02n3ejoc849u3dhu1blihnv.png)
2. Calculate v:
![\[ v = \sqrt{(k)/(m) x} \]](https://img.qammunity.org/2024/formulas/physics/college/o0zaiehjsgeo5b7grbtg6tuj9w5u94ymim.png)
![\[ v = \sqrt{\frac{800 \, \text{N/m}}{0.150 \, \text{kg}} * 0.108 \, \text{m}} \]](https://img.qammunity.org/2024/formulas/physics/college/szjy1n43sicr7bhikjs90ynf64jzct9l9l.png)
Calculating v:
![\[ v \approx 4.16 \, \text{m/s} \]](https://img.qammunity.org/2024/formulas/physics/college/syqgy0cwxk4mww6eop8h9xqp1jaxg7zf09.png)
3. Calculate t:
![\[ t = (v)/(g) \]](https://img.qammunity.org/2024/formulas/physics/college/1jd41g7avfdzm0dw9xfsxy9wuzrx16iq9g.png)
![\[ t = \frac{4.16 \, \text{m/s}}{9.8 \, \text{m/s}^2} \]](https://img.qammunity.org/2024/formulas/physics/college/uphkm65a4sbp3oz76amx2wkkiskpvppx73.png)
Calculating t:
![\[ t \approx 0.425 \, \text{s} \]](https://img.qammunity.org/2024/formulas/physics/college/ais4vb9runm329nodjb4iw384g9htqk7ld.png)
4. Calculate h:
![\[ h = (1)/(2) g t^2 \]](https://img.qammunity.org/2024/formulas/physics/high-school/2lvvyobywy8bivsbbpehpeigecl2pahmue.png)
![\[ h = (1)/(2) * 9.8 \, \text{m/s}^2 * (0.425 \, \text{s})^2 \]](https://img.qammunity.org/2024/formulas/physics/college/nfl764pxq23vbfvnwc7nd0q0lre0o989ep.png)
Calculating h:
![\[ h \approx 0.924 \, \text{m} \]](https://img.qammunity.org/2024/formulas/physics/college/gsg37io7iwloom2rtsflw13x9ypifv1j5w.png)
Therefore, the maximum height gained by the cube is approximately
 above its initial position.
above its initial position.