Question

Find the term in x^9 in the expansion of 11 3 - 3 X​

Answer 1

Using the binomial theorem to find the term in x^9 in the expansion of (x^3-3/x)^11 is:
`55 * x^(27) * 9/x^2 = 495x^{25`.

The binomial theorem states that for any non-negative integer n:

`(x + y)^n = C(n,0)x^n*y^0 + C(n,1)x^(n-1)*y^1 + C(n,2)x^(n-2)y^2 + ... + C(n,n)x^0y^n`

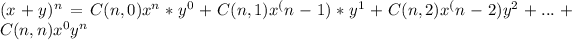
where C(n, k) represents the binomial coefficient "n choose k".

In our case, we have (x^3 - 3/x)^11. We can rewrite this as
`(x^3 - 3x^{(-1))^{11`.

Using the binomial theorem, the term in x^9 in the expansion will occur when we choose the x^3 term from each of the 9 factors of (x^3)^9, and the -3/x term from the remaining 2 factors of (-3/x)^2.

So, the term in x^9 is given by: C(11, 2) * (x^3)^9 * (-3/x)^2

C(11, 2) = 55 (x^3)^9 = x^27 (-3/x)^2 = 9/x^2

Thus, the term in x^9 in the expansion of (x^3-3/x)^11 is:
`55 * x^(27) * 9/x^2 = 495x^{25`.

Complete Question:

Find the term in x^9 in the expansion of (x^3-3/x)^11