Question

I need the steps to the equation there is a part c but I wasn’t able to fit it in

Answer 1

We can see in the graph that f(x) and g(x) are parallel lines. This means that to transform f(x) into g(x), we can shift it horizontally or vertically.

Part A: Applying a vertical or horizontal shift to f(x) will result in g(x).

For part B, we need to find the transformations.

We can take two points of each function:

f(x): (0, -10) and (5, 0)

g(x): (0, 6) and (-3, 0)

Then, if we apply vertical shift in (0, -10), we should get the point (0, 6). Then, we can solve:

`\begin{gathered} -10+k=6 \\ k=6+10 \\ k=16 \end{gathered}`

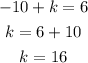
If we apply a horizontal shift, the point (5, 0) should transform into (-3, 0). Then:

`\begin{gathered} 5+k=-3 \\ k=-3-5 \\ k=-8 \end{gathered}`

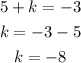
Part B:

Horizontal shift: k = -8

Vertical shift: k = 16

For part C we need to write an equation for each transformation.

Given a function h(x), a vertical shift of k units is written:

`vertical\text{ }shift\text{ }k\text{ }units=f(x)+k`

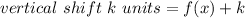
And a horizontal shift of k units:

`horizontal\text{ }shift\text{ }k\text{ }units=f(x-k)`

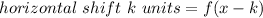
Vertical shift: This transformation adds 16 units in the y-coordinate.

`g(x)=f(x)+16`

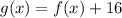
Horizontal shift: This transformation subtracts 8 from the x-coordinate:

`g(x)=f(x+8)`