Partial quotients involve breaking down a square root expression into parts to simplify the division. Let's go through the process for each:
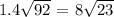
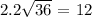
3.

4.
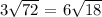
5.
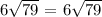
6.
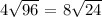
7.
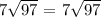
8.
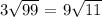
Partial quotients involve breaking down a square root expression into parts to simplify the division. Let's go through the process for each:
![1. \(4√(92)\) 4√(92) = 4√(4 * 23) = 8√(23)\]\\2. \(2√(36)\) 2√(36) = 2 * 6 = 12\]\\3. \(5√(76)\) 5√(76) = 5√(4 * 19) = 10√(19)\]\\4. \(3√(72)\) 3√(72) = 3√(4 * 18) = 6√(18)\]\\](https://img.qammunity.org/2024/formulas/mathematics/high-school/6mi4wku98m7cuuwksryjxjgt2jbbje4f5r.png)
![5. \(6√(79)\) 6√(79)\] (No perfect square factors, so it remains in radical form)\\6. \(4√(96)\) 4√(96) = 4√(4 * 24) = 8√(24)\]\\7. \(7√(97)\) 7√(97)\] (No perfect square factors, so it remains in radical form)\\8. \(3√(99)\) 3√(99) = 3√(9 * 11) = 9√(11)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qw7jvaewatatk1doj7504w22euovvt1a8k.png)
These results represent the simplified forms of the given square root expressions using partial quotients.