To determine wich coordinates points match up with the equations you have to replace said equations with the x-coordinate and see if the result is equal to the y-coordinate.
First point (0,0)
x=0 and y=0
1st equation
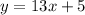
Replace it with x=0

This point doesn't match up with this equation.
2nd equation
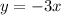
Replace with x=0
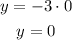
This point matches up with the equation.
3rd equation
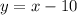
Replace with x=0
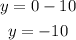
This point doesn't match up with this equation.
Result, the point (0,0), called origin, matches up with the equation in the second column.
Second point (8,-2)
x=8 y=-2
First equation
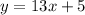
Replace with x=8
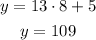
This point doesn't match up with this equation.
Second equation
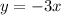
Replace with x=8
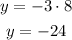
This point doesn't match up with this equation.
Third equation
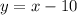
Replace with x=8

This point matches up with the equation.
Result, the point (8,-2), matches up with the equation in the third column.