Question

Earth’s orbits once around the sun every 365.25 days at an average radius of 1.5x10^11m. Earth’s mass is 6x10^24kg. a) what distance does earth travel in 1 year?b) what is earths average centripetal acceleration?c) what is the average force that the sun exerts on earth?

Answer 1

distance = 9.42 x 10^11 m

Acceleration = 5.94 x 10^-3 m/s2

Force = 3.56 x 10^22 N

Step-by-step explanation:

Part a)

The distance travel by the earth in 1 year can be calculated as the circumference of a circle of radio r, so:

`\begin{gathered} d=2\pi r \\ d=2(3.14)(1.5*10^(11)m) \\ d=9.42*10^(11)m \end{gathered}`

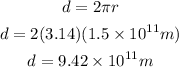
So, the distance is 9.42 x 10^11 m

Part b)

The centripetal acceleration can be calculated as:

`a_c=(v^2)/(r)`

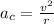
Where v is the velocity and r is the radius of the earth. So, the velocity is equal to:

`v_{}=\frac{\text{distance}}{\text{time}}=\frac{9.42*10^(11)m}{365.25\text{days x 24 hr x 60 min x 60 s}}=29850.18\text{ m/s}`

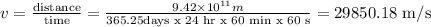
Therefore, the centripetal acceleration is:

`a_c=((29850.18)^2)/(1.5*10^(11))=5.94*10^(-3)m/s^2`

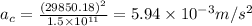
Part c)

Finally, the average force that the sun exerts on the earth can be calculated by the second law of Newton as:

`\begin{gathered} F=m\cdot a_c \\ F=(6*10^(24))\cdot(5.94*10^(-3)) \\ F=3.56*10^(22)\text{ N} \end{gathered}`

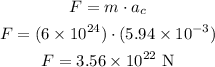
Therefore, the answers are:

distance = 9.42 x 10^11 m

Acceleration = 5.94 x 10^-3 m/s2

Force = 3.56 x 10^22 N