Our arrange looks like the following:
The potential energy in each individual point is given by:
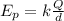
As all points have the same distance from the center of the square, we can calculate a single distance. We'll need the pythagorean theorem in order to calculate the distance. It can be written as the following
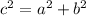
Then we can calculate this using half the side of the square. We get
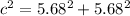
By isolating c we can find
![c=\sqrt[2]{5.68^2+5.68^2}=8.03cm](https://img.qammunity.org/qa-images/2023/formulas/physics/college/c3b34edzcwiz9lazzrvo.png)
This is the distance from each vertex to the center
We also need to take into account the fact that the total potential energy is the sum of potential energies
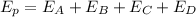
It can then be written as
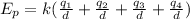
Which, once we plug our values in, yields:
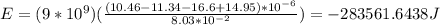
Thus, our final answer is 283561.6438J