The area of a circle is given by:
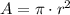
The raindrop hitting is represented as a function for the radius that grows with the time, which is given by:
![r(t)=20\sqrt[]{t+2}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/zsczcx0w9ew7ezao3xtk.png)
Looking at both equations, we can deduce that they correspond to each other by the radius, so we need to relate both equations taking into consideration that we need to find the area of the circle ripple, therefore:
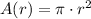
We can relate both equations using composed functions A(r(t)), in this case, the function of the area in terms of the function of the ripples radius:
![A(r(t))=\pi\cdot(20\sqrt[]{t+2})^2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/c7ghj5gro67rahe23eej.png)
Now, we need to find the area of the ripple at t=2, so we replace t=2 on the composed function:
![A(r(t))=\pi\cdot(20\sqrt[]{2+2})^2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/t2sfd8j5wb24f4oia38s.png)
![A(r(t))=\pi\cdot(20\sqrt[]{4})^2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/xf3v6pdmn1yj2jctvlom.png)
![A(r(t))=\pi\cdot(20\sqrt[]{4})^2](https://img.qammunity.org/qa-images/2023/formulas/mathematics/high-school/xf3v6pdmn1yj2jctvlom.png)
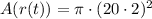
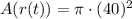
Finally:
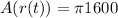
or
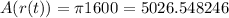
Where the area is given in inches square.