Question

A hanging wall picture is in the shape of a rhombus. The width of the picture is 10 inches. A diagonal side length is 8 inches. How tall is the picture?

Answer 1

`2√(39)` inches

Explanation:

1. We can use the Pythagorean theorem to solve for half of the height of the picture:
`a^(2) +b^(2) =c^(2)`

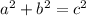
2. If the rhombus is cut in fourths by cutting from corner to corner, then 4 right-angled triangles are formed. Based on the information given, we can conclude that a triangle

• Has a hypotenuse of 8 inches (the diagonal side)
• And one of the other sides is 5 (half of the width of the picture, which is 10)

3. Knowing this information, we can identify values that can be plugged into the Pythagorean theorem to solve for the last side.

• c = 8
• a = 5
• b = ? (we are solving for it)

4. Plug the values into the Pythagorean theorem and solve for b.

• Plug in the values:
  `5^(2) +b^(2) =8^(2)`
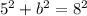
• Apply the exponents:
  `25 +b^(2) =64`
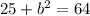
• Subtract 25 from both sides:
  `b^(2) =39`
• Square root both sides:
  `b=√(39)`

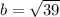
5.
`√(39)` is only half of the height of the picture, since we were solving for a side of the triangle. To find the full length, we multiply it by 2. Therefore, the picture is
`2√(39)` inches tall.