Question

A wind turbine uses the power of wind to generate electricity. The blades of the turbine make a

noise that can be heard at a distance from the turbine. At a distance of d=0 meters from the
turbine, the noise level is 105 decibels. At a distance of d = 100 meters from the turbine,
noise level is 49 decibels.
the
The noise level can be modeled by the function S given by S(d) = abd, where S(d) is the
noise level, in decibels, at a distance of d meters from the turbine.

Answer 1

The first equation is a = 105 and the second second equation is
`a * b^1^0^0 = 49.`

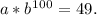
The values for a and b are:

a = 105 and b ≈ 0.972.

How to write equations

(i) We can use the given data to write two equations using the function

`S(d) = ab^d`

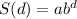
At a distance of d = 0 meters, the noise level is S(0) = 105 decibels:

S(0) =
`ab^0` = a * 1 = a

Therefore, the first equation is a = 105.

At a distance of d = 100 meters, the noise level is S(100) = 49 decibels:

S(100) =
`ab^1^0^0`

Since we want to find the values for constants a and b, we can rewrite the equation as:

`49 = a * b^1^0^0`

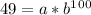
This gives us the second equation:
`a * b^1^0^0 = 49.`

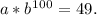
(ii) Now, find the values for a and b using the equations we derived:

From the first equation, we know that a = 105.

Substituting this value into the second equation:

105 * b¹⁰⁰ = 49

To isolate b, we divide both sides of the equation by 105:

b¹⁰⁰ = 49 / 105

Taking the 100th root of both sides to solve for b:

b = (49 / 105)^(1/100)

Using a calculator, evaluate this expression:

b ≈ 0.992

Therefore, the value of b is approximately 0.992.

Substituting the value of b back into the first equation:

a = 105

So, the values for a and b are:

a = 105 and b ≈ 0.972.