I'll do the first 6 rows to get you started.
===========================================
In row 1, we have the number
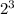 which is the same as writing 2^3
which is the same as writing 2^3
The base is 2 and the exponent is 3. Think of "base" as in "basement" to remember that the base is under the exponent. The exponent tells us how many copies of the base to multiply out. In this case, we have three copies of the base "2" multiplied to get 2*2*2 = 8
============================================
In row 2, we have the number 3^2. The base is 3 and the exponent is 2.
We can say 3^2 = 3*3 = 9. We have two copies of the base multiplied. Think of a 3 inch by 3 inch square that has area of 9 square inches.
============================================
Row 3:
The number 5^4 means 5^4 = 5*5*5*5 = (5*5)*(5*5) = 25*25 = 625
The base is 5 and the exponent 4 tells us how many copies of the base to multiply.
============================================
Row 4:
We aren't given the number like in the earlier rows. But we can see that the base is 6 and the exponent is 2. So the number to fill in that first blank is 6^2
The expanded notation would be 6*6 because the exponent tells us how many copies of the base to multiply out.
The standard notation is 36 because 6*6 = 36.
============================================
Row 5:
This time we don't have an exponent, but we have the base and we have the expanded notation.
The expanded notation of 8*8*8 means the base is 8 and the exponent is 3
So 8^3 = 8*8*8 = 512
We'll have 8^3 to fill in the first blank of row five, 3 fill in the next blank, and finally 512 fill in the last blank.
============================================
Row 6:
We have six copies of '9' multiplied together
This tells us we have the number 9^6. The base is 9 and the exponent is 6
Use your calculator to determine that 9^6 = 9*9*9*9*9*9 = 531441
============================================
I'll let you do the rest of the remaining rows.