Question

Two identical strings making an angle of 0= 26.3 degree with respect to the vertical support a block of mass m=13.7 Kg what is the tension in each of the strings ?

Answer 1

The free-body diagram of the configuration shown is the following:

Now, we add the forces in the vertical direction:

`\Sigma F_v=T_y+T_y-mg`

Since the system is in equilibrium the sum of forces in the vertical direction is zero:

`T_y+T_y-mg=0`

Now, we add like terms:

`2T_y-mg=0`

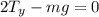
Now, the y-component of the tension is determined using the following right triangle:

Now, we use the trigonometric function cosine:

`cos(26.3)=(T_y)/(T)`

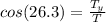
Now, we multiply both sides by "T":

`Tcos(26.3)=T_y`

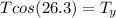
Now, we substitute in the sum of vertical forces:

`2Tcos(26.3)-mg=0`

Now, we solve for "T". First, we add "mg" to both sides:

`2Tcos(26.3)=mg`

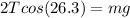
Now, we divide both sides by "2cos(26.3)":

`T=(mg)/(2cos(26.3))`

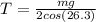
Now, we plug in the values of mass and the acceleration of gravity:

`T=((13.7kg)(9.8(m)/(s^2)))/(2cos(26.3))`

Now, we solve the operations:

`T=74.88N`

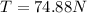
Therefore, the tension is 74.88 Newton