Question

Tell whether the orthocenter is inside, on, or outside the triangle. Then find the coordinates of the orthocenter.

L(0,5), M(3,1), N(8,1): Is it outside, inside or on?

The orthocenter is ( , )

Answer 1

The orthocenter is outside the triangle, at (0, -5)

Explanation:

The orthocenter is the intersection of the altitudes. So let's find the slope-intercept equation of "LM" "MN" and "LN" then determine it's perpendicular:

LM: slope = m = 1-5/3-0 = -4/3, equation => y = -4/3x + 5, perpendicular => y = 3/4x + b

this line passes through the opposite point, (8, 1)...therefore we can find b:

y = 3/4x + b

1 = 3/4(8) + b, b = -5, equation => y = 3/4x - 5

______________________________________

MN: slope = m = 1-1/8-5 = 0, equation => y = 1, perpendicular => x = ?

the line passes through the opposite point (0, 5)...so we can find ? or b:

x = ?, equation => x = 0

______________________________________

LN: slope = m = 1-5/8-0 = -4/8 = -1/2, equation => y = -1/2x + 5, perpendicular => y = 2x + b

the line passes through the opposite point (3, 1)...so we can find b:

1 = 2(3) + b, b = 1-6 = -5, equation => y = 2x - 5

______________________________________

System of Equations:

`\begin{bmatrix}y=(3)/(4)x-5\\ y=2x-5\\ x=0\end{bmatrix}`

`\mathrm{Substitute\:}y=(3)/(4)x-5: \begin{bmatrix}x=0\\ (3)/(4)x-5=2x-5\end{bmatrix}`

`\mathrm{Substitute\:}x=0: \begin{bmatrix}(3)/(4)\cdot \:0-5=2\cdot \:0-5\end{bmatrix}`

`\mathrm{Simplify\:}: \begin{bmatrix}-5=-5\end{bmatrix}`

`\mathrm{For\:}y=(3)/(4)x-5,\\\mathrm{Substitute\:}x=0,\\y=(3)/(4)\cdot \:0-5 = -5`

`y=-5,\:x=0`

_____________________________________

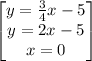
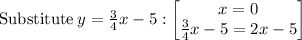
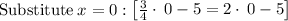
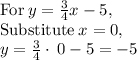
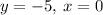
The orthocenter is outside the triangle, at (0, -5)

Answer 2

see explanation

Explanation:

The orthocentre is

• Inside all acute triangles

• Outside all obtuse triangles

• On all right triangles

To determine if the triangle is any of the above, we require the lengths of the 3 sides of the triangle.

Calculate the lengths using the distance formula

d =
`\sqrt{(x_(2)-x_(1))^2+(y_(2)-y_(1))^2 }`

L(0, 5) and M(3, 1)

LM =
`√((3-0)^2+(1-5)^2)` =
`√(3^2+(-4)^2)` =
`√(9+16)` =
`√(25)` = 5

L(0, 5) and (N(8, 1)

LN =
`√((8-0)^2+(1-5)^2)` =
`√(8^2+(-4)^2)` =
`√(64+16)` =
`√(80)` = 4
`√(5)`

M(3, 1) and (N(8, 1)

MN =
`√((8-3)^2+(1-1)^2)` =
`√(5^2+0^2)` =
`√(25)` = 5

Given 3 sides of a triangle a, b, c where c is the longest side, then

• a² + b² = c² ⇒ right triangle

• a² + b² < c² ⇒ acute triangle

• a² + b² > c² ⇒ obtuse triangle

Here a = 5, b = 5, c = 4
`√(5)`

a² + b² = 5² + 5² = 25 + 25 = 50

c² = (4
`√(5)` )² = 80

Since a² + b² < c² then triangle is obtuse and the orthocentre is outside the triangle.

The orthocentre is the point of intersection of the 3 Altitudes of the triangle.

We only require to find the equation of 2 of the altitudes and solve them simultaneously to obtain the coordinates of the orthocentre.

An Altitude is a line from a vertex at right angles to the opposite side

Altitude from M to LN

Calculate the slope of LN using the slope formula

m =
`(y_(2)-y_(1) )/(x_(2)-x_(1) )` =
`(1-5)/(8-0)` =
`(-4)/(8)` = -
`(1)/(2)` ⇒
`m_(perpendicular)` = 2

Equation of altitude

y - 1 = 2(x - 3)

y - 1 = 2x - 6

y = 2x - 5 → (1)

Altitude from N to LM

m =
`(1-5)/(3-0)` = -
`(4)/(3)` ⇒
`m_(perpendicular )` =
`(3)/(4)`

Equation of altitude

y - 1 =
`(3)/(4)`(x - 8)

y - 1 =
`(3)/(4)` x - 6

y =
`(3)/(4)` x - 5 → (2)

Equating (1) and (2)

2x - 5 =
`(3)/(4)` x - 5 ( multiply through by 4 )

8x - 20 = 3x - 20

5x - 20 = - 20 ( add 20 to both sides )

5x = 0 ⇒ x = 0

Substitute x = 0 into (1)

y = 0 - 5 = - 5

The orthocentre is (0, - 5 )