Question

Hello! I need some assistance with this homework question I have. The image is posted below Q5

Answer 1

From the problem, we have :

`f(x)=x^2+8x-32`

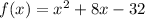
Set f(x) = 0 :

`0=x^2+8x-32`

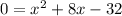
Add 32 to both sides of the equation :

`\begin{gathered} 32=x^2+8x-32+32 \\ 32=x^2+8x \end{gathered}`

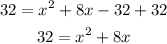
Next is to add a number to both sides of the equation using the formula (b/2a)^2

That will be :

`((b)/(2a))^2=((8)/(2))^2=16`

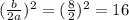
The equation will be :

`\begin{gathered} 32+16=x^2+8x+16 \\ 48=x^2+8x+16 \end{gathered}`

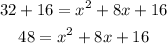
Take note that the right side of the equation is now a perfect square trinomial and we can factor it by :

`\begin{gathered} 48=x^2+8x+16 \\ 48=(x+4)^2 \\ (x+4)^2=48 \end{gathered}`

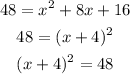
Take the square root of both sides :

`\begin{gathered} \sqrt[]{(x+4)^2}=\sqrt[]{48} \\ x+4=\pm4\sqrt[]{3} \end{gathered}`

Subtract 4 to both sides of the equation :

`\begin{gathered} x+4-4=-4\pm4\sqrt[]{3} \\ x=-4\pm4\sqrt[]{3} \end{gathered}`

Take note that zeros and x-intercepts are the same.

Therefore, the answer is :

A. The zeros and the x-intercepts are the same. They are -4 + 4√3 and -4 - 4√3