Question

In 1994, the moose population in a park was measured to be 3780. By 1999, the population was measured again to be 3180. If the population continues to change linearly: A.) Find a formula for the moose population, P, in terms of t, the years since 1990. B.) What does your model predict the moose population to be in 2006?

Answer 1

A. P = -120t + 4260

B. P = 2340

Step-by-step explanation:

A linear equation of the population P in terms of t, the years since 1990 will have the form:

P = mt + P0

Where P0 is the population when t is 0 or the population in 1990 and m is the slope. So, we can find the equation using the ordered pairs (x1, y1) =(4, 3780) and (x2, y2) = (9, 3180) as:

`\begin{gathered} P=\frac{P_2-P_1}{t2_{}-t_1}(t-t_1)+y_1 \\ P=(3180-3780)/(9-4)(t-4)+3780 \\ P=(-600)/(5)(t-4)+3780 \\ P=-120(t-4)+3780_{} \\ P=-120t+480+3780 \\ P=-120t+4260 \end{gathered}`

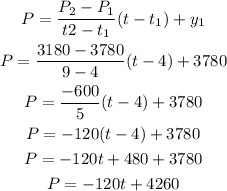
Now, we can calculate the population in 2006, replacing t by 16 because:

2006 - 1990 = 16

So, the population is equal to:

`\begin{gathered} P=-120t+4260 \\ P=-120(16)+4260 \\ P=2340 \end{gathered}`