Question

A kangaroo jumps at 6.32 m/s from flat ground at a 55.8° angle. How long does it take to reach its maximum height? (Unit = s) ​

Answer 1

0.533 s

Step-by-step explanation:

To solve for the time it takes for a kangaroo to reach its maximum height, we'll use principles of projectile motion. The initial velocity of the kangaroo is 6.32 m/s at a 55.8° angle. We're interested in the vertical component of this velocity, as it determines the time to reach the maximum height.

`\boxed{\left\begin{array}{ccc}\text{\underline{The 4 Kinematic Equations:}}\\\\1. \ \vec v_f=\vec v_0+\vec at\\\\2. \ \Delta \vec x=(1)/(2)(\vec v_f-\vec v_0)t\\\\3. \ \Delta \vec x=\vec v_0t+(1)/(2)\vec at^2\\\\ 4. \ \vec v_f^2=\vec v_0^2+2\vec a \Delta \vec x \end{array}\right}`

`\hrulefill`

To calculate the vertical component of the velocity, We'll use the initial velocity, the angle, and the following equation:

`\Longrightarrow \vec v_(0_y)=\vec v_0\sin(\theta)\\\\\\\\\Longrightarrow \vec v_(0_y)=(6.32 \ m/s)\sin(55.8 \textdegree)\\\\\\\\\therefore \vec v_(0_y) \approx 5.227 \ m/s`

Now that we know vertical component of velocity, we can calculate the time to reach the maximum height. At the maximum height, the vertical velocity becomes zero. So we will use the first kinematic equation from above.

`\Longrightarrow \vec v_(f_y)=\vec v_(0_y)+\vec a_yt`

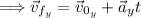
Where:

• v_fy = 0 m/s
• v_0x = 5.227 m/s
• a_y = -9.8 m/s² (acceleration due to gravity)

Substitute in these values and solve for 't':

`\Longrightarrow0=5.227+(-9.8)t\\\\\\\\\Longrightarrow -9.8t=-5.227\\\\\\\\\therefore t \approx \boxed{0.533 \ s}`

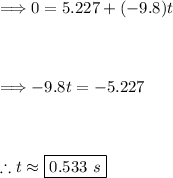
Thus, it takes the kangaroo approximately 0.533 seconds to reach its maximum height.