ANSWER:
f(x) is an exponential function
g(x) is neither linear nor exponential
h(x) is a linear function
Explanation:
The function f(x) we can notice that it is decreasing at a rate that is not constant, but we must calculate the ratio of decrease, if it is constant it is an exponential function:
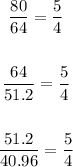
Which means that f(x) is an exponential function
The function g(x) also decreases non-constantly, we calculate the ratio:
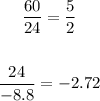
The ratio is not constant which means that the function g(x) is neither linear nor exponential
The function h(x) decreases constantly, it decreases by 20 per unit, which means that it is a linear function