Question

Logan has two aquariums. One aquarium contains 2.1 cubic feet of water and the other contains 1.4 cubic feet of water. The water in the larger aquarium weighs 43.68 pounds more than the water in the smaller aquarium. Complete the equation with a variable on both sides to represent the situation. Use x to represent the weight of 1 cubic foot of water. Then find the weight of 1 cubic foot of water.

Answer 1

Given in the question:

a.) One aquarium contains 2.1 cubic feet of water.

b.) The other aquarium contains 1.4 cubic feet of water.

c.) The water in the larger aquarium weighs 43.68 pounds more than the water in the smaller aquarium.

To be able to answer this type of problem, we will be applying the ratio and proportion:

We get,

`\frac{Wt\text{. of Large Aquarium}}{Volume\text{ of Large Aquarium}}\text{ = }\frac{Wt.\text{ of Small Aquarium}}{Volume\text{ of Small Aquarium}}`
`\text{ }\frac{\text{ w + 43.68 lbs.}}{2.1ft.^3}\text{ =}\frac{\text{ w}}{1.4ft.^3}\text{ }\rightarrow\text{ }\frac{w\text{ + 43.68}}{2.1}\text{ = }(w)/(1.4)`
`\frac{w\text{ + 43.68}}{2.1}\text{ = }(w)/(1.4)`
`(w\text{ + 43.68)}(1.4)\text{ = (}w)(2.1)`
`\text{ 1.4w + }61.152\text{ = 2.1w}`
`\text{2.1w = 1.4w + }61.152`

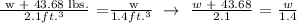
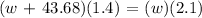
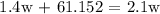
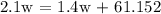
Therefore, the equation is 2.1w = 1.4w + 61.152

Let's determine the value of w:

`\text{2.1w = 1.4w + }61.152`
`\text{2.1w - 1.4w = }61.152`
`0.7\text{w = }61.152`
`\frac{0.7\text{w }}{0.7}\text{= }(61.152)/(0.7)`
`\text{ w = }87.36\text{ lbs.}`

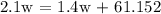
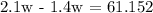
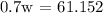
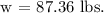
Let's determine the weight of 1 cubic foot of water:

`\text{ Wt. of 1 ft}^3\text{ of water = }\frac{Wt.\text{ of Small Aquarium}}{Volume\text{ of Small Aquarium}}`
`\text{ = }\frac{87.36\text{ lbs.}}{1.4ft.^3}`
`\text{ = }62.4lbs./ft^3`

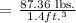
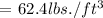
Therefore, the weight of 1 cubic foot of water is 62.4 lbs.