Question

Determine whether the graphs of the given equations are parallel, perpendicular, or neither.

Y= -2x+3
2x+y=7
A. Parallel
B. Perpendicular
C. Neither

Answer 1

Parallel

Explanation:

If lines have the same slope, then they are parallel. If lines have slopes that are opposite reciprocals of each other, then they are perpendicular. If neither one of those statements are true, then the answer is neither.

1) First, find the slope of the first equation.
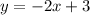`y = -2x + 3` is already in
`y = mx + b` format, or slope-intercept form. The
`m`, or the coefficient of the x term, represents the slope. Thus, by looking at the equation, -2 is the slope of
`y = -2x + 3`.

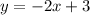2) Second, find the slope of the second equation.
`2x + y = 7` is in standard format, but we can change it to slope-intercept format by isolating the y like so (just subtract both sides by 2x):

`2x + y = 7 \\y = -2x + 7`

Now that it is in slope-intercept form, we can look at the coefficient of the x term, or
`m`, to find the slope. That number is -2, thus the slope of
`2x + y = 7` is -2.

3) We found out that the slopes of both equations are -2. Thus, since they share the same slope, the lines are parallel.

Answer 2

A

Explanation:

Because the have the same slope.

The second equation solving for y is:

Y= -2x+7.

Both equations have the same slope of -2