Answer:
r = 5.848cm, h = 11.696cm
Explanation:
Surface area:
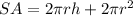
Volume:
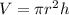
Therefore, the height of a cylinder given its volume would be
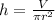 , thus:
, thus:
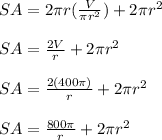
We now find the derivative of the surface area of the cylinder with respect to its radius and set it equal to 0, solving for the radius:
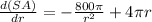
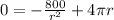
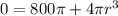
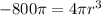
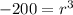
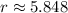
If
![0If [tex]r>5.848](https://img.qammunity.org/2023/formulas/mathematics/high-school/9f9a05gibowh0bk0wg1ka4ug0v3k7q9mqg.png) , then the surface area of the cylinder increases
, then the surface area of the cylinder increases
Therefore, the surface area is minimized when the radius is
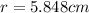 , making the minimum height
, making the minimum height
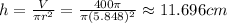 .
.
In conclusion, the 2nd option is correct.