Question

Solve the inequalities by graphingy> 2 xy< 3

Answer 1

See the picture in the explanation

Explanation

Given the inequalities:

`\begin{gathered} y\gt2x \\ y\lt3 \end{gathered}`

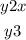
First, we need to draw the line: y = 2x. Substituting x = 0 and x = 1 we can get two points on the line, as follows:

`\begin{gathered} y=2(0)=0 \\ y=2(1)=2 \end{gathered}`

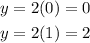
Then, connecting the points (0, 0) and (1, 2) the line y = 2x is drawn.

Next, we need to substitute a point in the inequality y > 2. Substituting gthe point )0, )1, we get:

`\begin{gathered} 1\gt2(0) \\ 1\gt0 \end{gathered}`

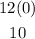
which is true. Then, the point (0, 1) is part of the solution of y > 2x. This means we need to shade the area above the line y = 2x. Given that a greater than symbol is used, the points on the line are not included in the solution of the inequality, in consequence, a dotted line must be used.

Next, we need to draw the line: y = 3. This is a line parallel to the x-axis that passes through the point (0, 3).

We need to substitute a point in the inequality y < 3. Substituting the point (0, 1), we get:

`1\lt3`

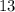
which is true. Then, the point (0, 1) is part of the solution of y < 3. This means we need to shade the area below the line y = 3. Given that a less-than symbol is used, the points on the line are not included in the solution of the inequality, in consequence, a dotted line must be used.

Combining this information, the solution to the inequalities is: