Question

John rolled a six sided die with the following results what was the meaning of the dies outcomes based on the frequency given round your answer to the two decimal places

Answer 1

Expected Value (or Mean Value)

A discrete random variable can have a specific number of outcomes, each one of which will have its own probability of occurrence.

Let's say the variable X is the possible outcome of the rolling of a six-sided die. The possible values for X are:

X = {1, 2, 3, 4, 5, 6}

Now we compute the probability of each event by dividing the frequency by the total number of experiences. The table provided in the question gives the frequencies as follows:

F = {12, 10, 12, 13, 9, 11}

For a total of n = 12 + 10 + 12 + 13 + 9 + 11 = 67 random experiences.

The expected value of a discrete random variable is calculated as the sum of the products of each possible outcome by its own probability.

For ease of calculations, we won't divide each frequency by n, but the total sum as follows:

`E_x=(1\cdot12+2\cdot10+3\cdot12+4\cdot13+5\cdot9+6\cdot11)/(67)`

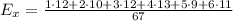
Calculating:

`\begin{gathered} E_x=(12+20+36+52+45+66)/(67) \\ E_x=(231)/(67) \\ E_x=3.45 \end{gathered}`

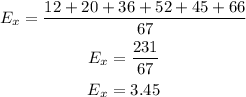
The mean of the dice outcomes is 3.45