Question

Suppose a population's doubling time is 19 years. Find its annual growth factor a and annual percent growth rate r.a=r=

Answer 1

Because populations grow exponentially, the equation for modelling the growth is:

`P(t)=P_0\cdot e^(a\cdot t)\text{.}`

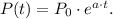
Where:

• P(t) is the population after t years,

,

• P_0 is the initial population,

,

• a is the growth factor.

To find the growth factor, we use the consider:

• t = 19 years,

,

• P(t) = 2 P_0 (we know that after t = 19 years the population will be doubled).

Replacing these data in the equation above and solving for a, we get:

`\begin{gathered} 2P_0=P_0\cdot e^{a\cdot19\text{ years}}, \\ (2P_0)/(P_0)=e^{a\cdot19\text{ years}}, \\ 2=e^{a\cdot19\text{ years}}, \\ \ln 2=a\cdot19\text{ years}\cdot\ln e \\ \ln 2=a\cdot19\text{ years}, \\ a=\frac{\ln2}{19\text{ years}}\cong\frac{0.03648}{\text{year}}\text{.} \end{gathered}`

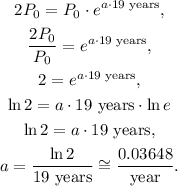
The annual percent growth rate r is:

`r=a\cdot100\%=\frac{0.03648}{\text{year}}.100\%=\frac{3.648\%}{\text{year}}\text{.}`

Answer

• a = 0.03648/year

,

• r = 3.648%/year