Question

If the population of a small town satisfies the exponential model A = 100.01st, where is measured in years, how long will it take for the town's population to increasefrom 5,100 to 6,120? Round your answer to two decimal places.AnswerKrynad

Answer 1

We are given that a population is modeled by the following function:

`A=A_0e^(0.015t)`

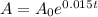
From this function, we can solve for the time "t". First, we divide both sides by A0:

`(A)/(A_0)=e^(0.015t)`

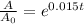
Now, we use the natural logarithm to both sides:

`ln((A)/(A_0))=ln(e^(0.015t))`

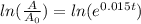
Now, we use the following property of logarithms:

`ln(x^y)=yln(x)`

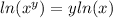
Applying the property we get:

`ln((A)/(A_0))=0.015tln(e)`

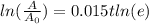
We have the following:

`ln(e)=1`

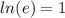
Substituting we get:

`ln((A)/(A_0))=0.015t`

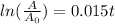
Now, we divide both sides by 0.015:

`(1)/(0.015)ln((A)/(A_0))=t`

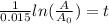
Now, the time it takes for the population to go from "A = 5100" to "A = 6120" we need to subtract the final time from the initial time, like this:

`(1)/(0.015)ln((6120)/(A_0))-(1)/(0.015)ln((5100)/(A_0))=t_f-t_0`

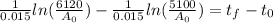
Now, we take "1/0.015" as a common factor:

`(1)/(0.015)(ln((6120)/(A_0))-ln((5100)/(A_0)))=t_f-t_0`

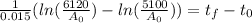
Now, we use the following property of logarithms:

`ln((x)/(y))=ln(x)-ln(y)`

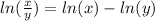
Applying the property we get:

`(1)/(0.015)(ln(6120)-ln(A_0)-ln(5100)+ln(A_0))=t_f-t_0`

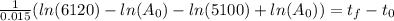
Now, we cancel out the "ln(A0)":

`(1)/(0.015)(ln(6120)-ln(5100))=t_f-t_0`

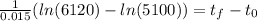
Solving the operations:

`12.15=t_f-t_0`

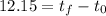
Therefore, the amount of time is 12.15 years.