SOLUTION
We want to factor
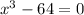
Looking at this, we can tell that (x - 4) or (x + 4) would be one of its factors, since 4 is a factor of 64. So let use check for (x - 4)
So, we will put x = 4 into the equation, we have
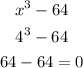
hence (x - 4) is a factor. Dividing the polynomial by (x - 4), we have
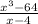
so we got

Factorizing the result, we have
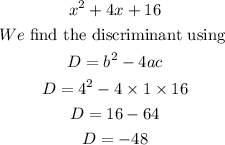
Now we have the discriminant, we use the formula to fin the roots of this equation, we have
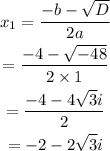
The second root becomes

Note that square root of -1 is i
So, comparing to the options, we can see that
The answer is option D