Question

Josephine wants to buy a new 48-inch-screen TV for her living room. She measures the width of the TV to be 42 inches. About how tall is the height of the TV, to the nearest tenth of an inch?

Answer 1

Imagine the following drawing for our situation. The TV's measurement are taken from one of the upper corners of the TV to the opposite lower corner of the TV. Then, imagine the TV as a rectangle. So we have the following drawing

As you can see, the height is the variable we want. And it forms a right triangle with the diagonal and the width of the tv. To solve for x, we will use pythagora's theorem. Which is as follows

Given a right triangle with sides a,b and c, the following equation follows.

`a^2+b^2=c^2`

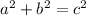
In our case c = 48 anc b = 42 and a=x. So the equation turns out to be

`x^2+42^2=48^2`

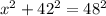
Now, if we subtract 42^2 on both sides, we get

`x^2=48^2-42^2`

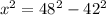
We finish up by taking the square root on both sides, so we get

`x\text{ = }\sqrt[]{48^2-42^2}\text{ = }\sqrt[]{2304\text{ - }1764}\text{ = }\sqrt[]{540}\text{ = }23.238\text{ inches}`

So the height of the tv is is about 23.238 inches